東大入試の理系数学で、2年連続 25点
ネタとしか思えない点数を入試本番で叩き出した元東大生の筆者が、十数年の時を超えて憎き数学にリベンジする。
「大学入試数学」カテゴリの記事では、その勉強プロセスを記録・公開しております。
(※ 計算ミスや論証ミスなどが有りましたら、コメント欄でご指摘ください。)
3次式(3乗)の因数分解の問題です。
問題
問題
\(a^3+b^3+c^3-3abc\) を因数分解せよ。
答案例・解説動画
答案例
解き方はいくつかパターンかあると思われますが、ここでは2パターンを掲載します。
3乗の因数分解といえば・・
\[ x^3+y^3 = \left(x+y\right)\left(x^2-xy+y^2\right) \]「対称式なので対称性を崩さずに」と考えて式変形していくと・・手こずると思います。
\[\hspace{15pt} a^3+b^3+c^3-3abc\] \begin{eqnarray} &=& \left(a^3+b^3\right)+c^3-3abc\\[5pt] &=& \left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc\\[5pt] &=& \left(a+b\right)^3+c^3-3ab\left(a+b+c\right)\\[5pt] &=& \left\{\left(a+b\right)+c\right\}\left\{\left(a+b\right)^2-\left(a+b\right)c+c^2\right\}-3ab\left(a+b+c\right)\\[5pt] &=& \left(a+b+c\right)\left\{\left(a^2+2ab+b^2-ca-bc+c^2\right)-3ab\right\}\\[5pt] &=& \left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right) \end{eqnarray}

\(x^3+y^2\) の因数分解の形をうまく利用した解法ですね

たまたま上手くいった感が否めないのは僕だけでしょうか
\[\quad \left(a+b+c\right)\left(a^2+b^2+c^2\right)\] \[=a^3+b^3+c^3+ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right) \]
よって、
\[\quad a^3+b^3+c^3-3abc\] \[ =\left(a+b+c\right)\left(a^2+b^2+c^2\right)-\left\{ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+3abc\right\} \tag{A} \]
ここで、
\[\quad \left(a+b+c\right)\left(ab+bc+ca\right)\] \[=ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+3abc\]
であるから、これを(A)に代入して
\[ \quad \left(a+b+c\right)\left(a^2+b^2+c^2\right)-\left\{ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+3abc\right\} \] \begin{eqnarray} &=& \left(a+b+c\right)\left(a^2+b^2+c^2\right)-\left(a+b+c\right)\left(ab+bc+ca\right)\\[5pt] &=& \left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right) \end{eqnarray}

これはインチキくさいですねw \(\left(a+b+c\right)\left(a^2+b^2+c^2\right)\) とか \( \left(a+b+c\right)\left(ab+bc+ca\right)\) とか、なんで唐突に出てきたんですか?

いや、上手くいくヤツを泥臭く探した結果です。
まず、\(\left(a+b+c\right)^3\) を展開してみました。
\[\left(a+b+c\right)^3=a^3+b^3+c^3+3\left\{ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+2abc\right\}\]
そして次に、余計な部分である \(ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\) のような項が出てくるような対称式の掛け算を探しました。
その結果見つかったのが、コレです。
\[\quad \left(a+b+c\right)\left(ab+bc+ca\right)\] \[=ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+3abc\]
でも、\(abc\) の符号と係数が合いません。色々と試行錯誤した結果、\(\left(a+b+c\right)\left(a^2+b^2+c^2\right)\) が見つかってくれました。
正直、見つかったのはたまたまですね。

いや、結局たまたまかいw
解説動画
まとめ・関連記事
因数分解って、ヒラメキというより「どれだけ多くのパターンを知っているか」が重要なんだと思います。
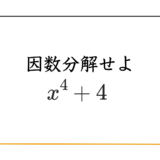
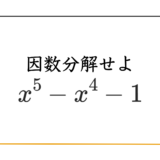
ということで、4次式の因数分解もついでにどうぞ