東大入試の理系数学で、2年連続 25点
ネタとしか思えない点数を入試本番で叩き出した元東大生の筆者が、十数年の時を超えて憎き数学にリベンジする。
「大学入試数学」カテゴリの記事では、その勉強プロセスを記録・公開しております。
(※ 計算ミスや論証ミスなどが有りましたら、コメント欄でご指摘ください。)
3次式や4次式の因数分解は、やり方を知らないと思いつかないものも多いですよね。
ということでこのページでは、4次式の因数分解の1パターンについてです。
ではさっそく問題です。
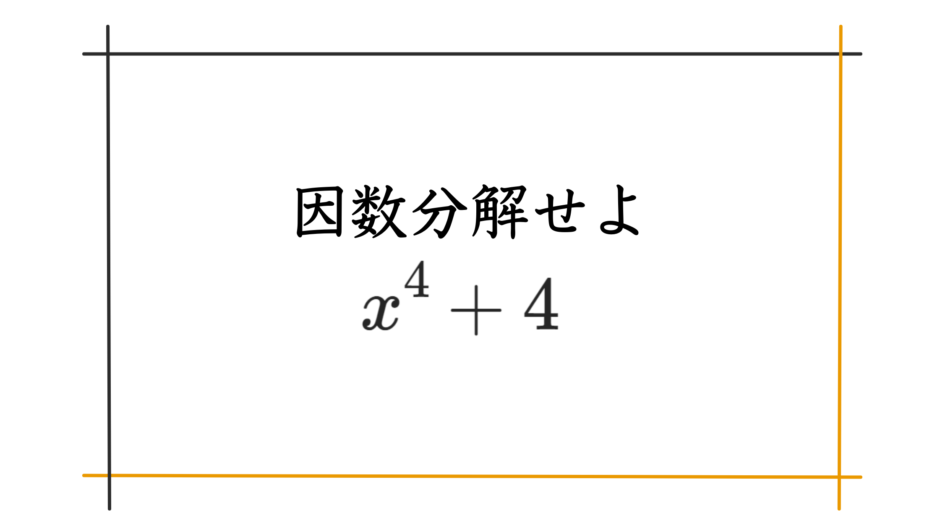
問題
\(x^4+4\) を因数分解せよ。
\[ \begin{align} \quad x^{4}+4 &=\left(x^{2}+2\right)^{2}-4x^{2} \\[3pt] &=\left(x^{2}+2\right)^{2}-\left(2x\right)^{2}\\[5pt] &=\left(x^2+2x+2\right)\left(x^2-2x+2\right) \end{align} \]

なんとかして「和と差の積( \(a^2-b^2\) )」の形にもっていく感じですね。
ソフィージェルマンの恒等式とは
上のような4次式の因数分解を一般化したものは、「ソフィージェルマンの恒等式」と呼ばれるそうです。
\[a^4+4b^4=\left(a^2+2ab+2b^2\right)\left(a^2-2ab+2b^2\right)\]
▼導出過程▼
\begin{eqnarray} a^4+4b^4 &=& \left(a^2+2b^2\right)^2-2\cdot2a^2b^2 \\[3pt] &=& \left(a^2+2b^2\right)^2-\left(2ab\right)^2 \\[5pt] &=& \left(a^2+2ab+2b^2\right)\left(a^2-2ab+2b^2\right) \end{eqnarray}
「4乗 + 4乗」のかたちで、片方の係数が4ならばこの公式が使えます。
たとえば、冒頭の \(x^4+4\) は \(4b^4\) の \(b\) に \(1\) を代入したものです。
他にも、
\begin{eqnarray} x^4+64 &=& \left(x^2+8\right)^2-16x^2 \\[3pt] &=& \left(x^2+8\right)^2-\left(4x\right)^2 \\[5pt] &=& \left(x^2+4x+8\right)\left(x^2-4x+8\right)\\[5pt] \end{eqnarray}
\begin{eqnarray} x^4+324p^4 &=& x^4+4\cdot81p^4 \\[5pt] &=& x^4+4\cdot3^4p^4 \\[5pt] &=& \left(x^2+2\cdot3^2p^2\right)^2-2\cdot2\cdot3^2p^2x^2 \\[5pt] &=& \left(x^2+18p^2\right)^2-\left(2\cdot3px\right)^2 \\[5pt] &=& \left(x^2+6px+18p^2\right)\left(x^2-6px+18p^2\right) \end{eqnarray}
などなど。
4次式の因数分解をしないといけない場面では、このソフィージェルマンの恒等式を思い浮かべながら、
「うまく和と差の積の形に持っていけないか?」と、まずは疑ってみると良いかもしれません。